프런트엔드 엔지니어를 위한 베지에 곡선(Bezier Curves) - 3편

2017.03.19

「프런트엔드 엔지니어를 위한 베지에 곡선(Bézier Curves) - 2편」을 포스팅한 후 시간이 꽤 지났다. 어디까지 이야기했더라? 기억도 가물가물하다. 최근에 강의를 시작하면서 여유가 없었다는 핑계를 대보지만, 뭐가 됐든 게을러서 그렇다. 3편을 기다리신 분이 있었다면 죄송할 따름이다.

글과 관련 없는 얘기는 이쯤 하자. 2편에서는 에버리징과 블렌딩 그리고 인터폴레이션(Interpolation)이라고 부르는 보간을 소개했다. 베지에 곡선을 이해하기 위한 기초 지식이었으며 이 개념만 이해하고 있으면 나머지는 쉽게 이해할 수 있다.

1차 베지에 곡선

우리는 이미 1차 베지에 곡선(Linear Bezier Cuvers)을 경험했다. 2편의 복합 데이터 블렌딩과 보간 절에서 보여준 예제가 바로 1차 베지에 곡선이다. 차이점이 있다면 단순히 평면상에서 곡선을 그리는 게 아니라 직교좌표계 상에서 그린다는 것이다.

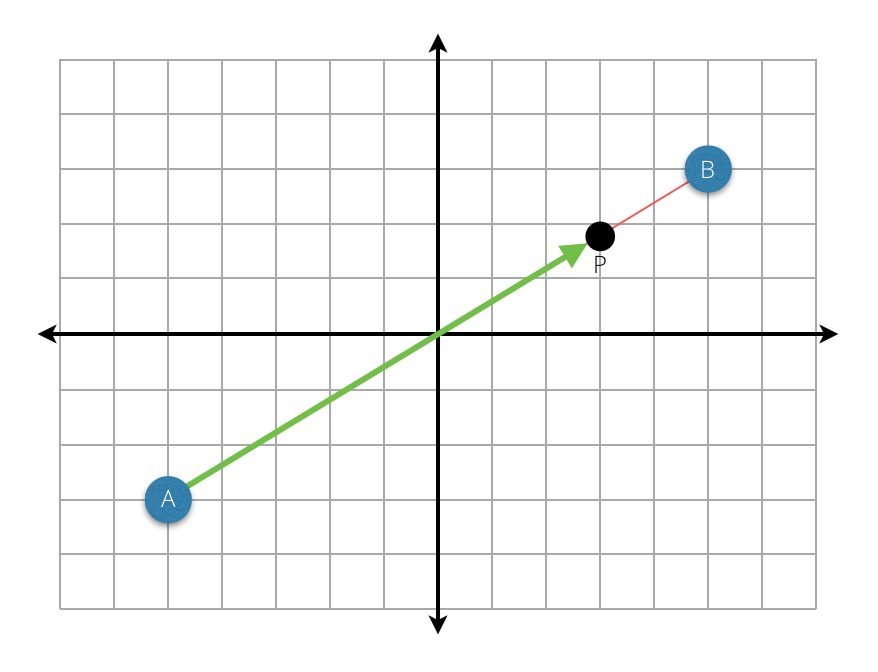
1차 베지에 곡선은 조절점(Control point) 두 개로 그린다. 아주 간단하지만, 굴곡이 없는 선형이다(직선도 곡선에 포함된다는 사실을 잊지 말자).

2차 베지에 곡선

그럼 2차 베지에 곡선(Quadratic Bézier Curves)을 그려보자. 2차 베지에 곡선은 조절점 3개를 이용해 그린 곡선을 말한다.

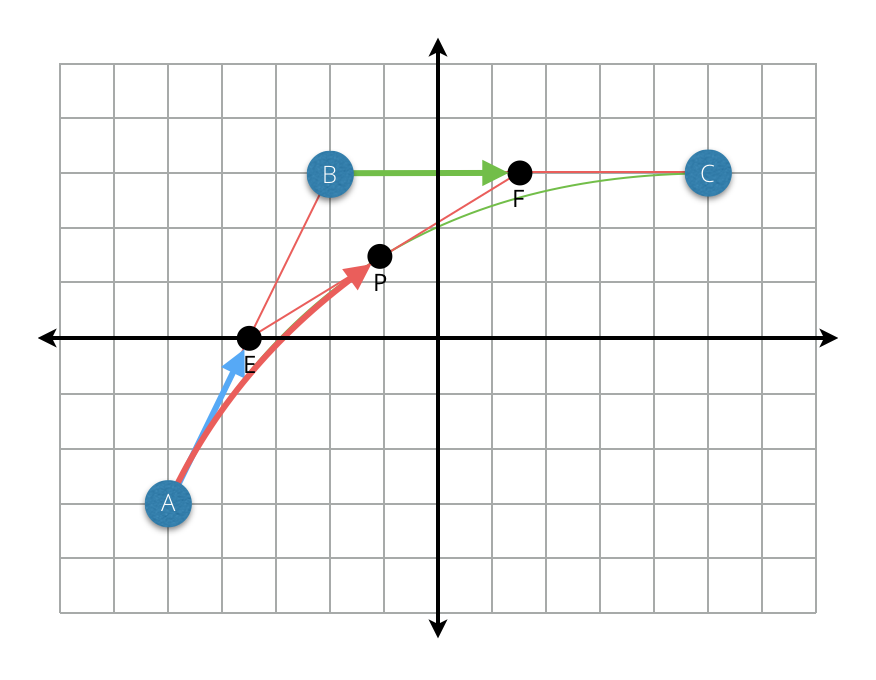
3개의 조절점 A, B, C를 이용해 그린 두 개의 직선 즉, 두 개의 1차 베지에 곡선이 있다. 그리고 이 곡선에서 보간되는 점 E와 F도 있다. 이때 점 E와 F를 이용해 또 다른 직선을 그릴 수 있고 이 직선에서 보간되는 점 P도 추가할 수 있다. 이제 점 E와 F 그리고 P를 보간하면 P의 행적이 곡선을 만들어 낸다(이해가 되지 않는다면 「중학생도 알 수 있는 베지에 곡선」을 참고한다).

그럼 이제 2차 베지에 곡선을 직접 그려보도록 하자. 선분에서 블렌딩 되는 점 P를 구하는 공식은 다음과 같다(자세한 내용은 「프런트엔드 엔지니어를 위한 베지에 곡선(Bézier Curves) - 2편」을 참고). 이때 s = 1 - t다.

P = (s * A) + (t * B)

그림 2를 보면 알 수 있듯이 2차 베지에 곡선을 그리기 위해서는 점 E와 F 그리고 P를 보간해야 한다. 점 E는 조절점 A와 B를 이용해 구할 수 있고, 점 F는 조절점 B와 C를 이용해 구할 수 있다. 그리고 점 P는 다시 점 E와 F를 이용해 구할 수 있다.

E = (s * A) + (t * B)
F = (s * B) + (t * C)
P = (s * E) + (t * F)

이 공식을 자바스크립트 코드로 옮겨보자. 여기에서는 구현에 있어 몇 가지 중요한 함수만 소개한다. 전체 코드는 코드펜(CodePen)에 작성해 놓은 예제를 참고한다.

먼저 blender()는 점 A와 점 B 그리고 가중치 t를 전달받아 블랜딩한 결괏값을 반환하는 함수다.

function blender(A, B, t) {
  if (t === 0) {
    return A;
  }

  if (t === 1) {
    return B;
  }

  return ((1 - t) * A) + (t * B); // or A + t * (B - A)
}

이때 blender()는 좌표 하나에 대한 연산만 책임지므로 x, y 좌표를 연산하기 위해 blend()를 작성한다.

function blend(x1, x2, y1, y2, t) {
  const x = blender(x1, x2, t);
  const y = blender(y1, y2, t);

  return {x, y};
}

다음으로 blend()를 이용해 점 A와 점 B의 좌표를 전달해 점 E의 좌푯값을 구하고 점 B와 점 C의 좌표를 전달해 점 F의 좌표를 구한다. 그리고 다시 점 E와 점 F의 좌표를 전달해 점 P의 좌표를 구하는 방식으로 공식을 구현한다.

interpolateBtn.addEventListener(\'click\', function() {
  // Start the interpolation.
  raf(function(t) {
    const posE = blend(posA.x, posB.x, posA.y, posB.y, t);
    const posF = blend(posB.x, posC.x, posB.y, posC.y, t);
    const posP = blend(posE.x, posF.x, posE.y, posF.y, t);
    ...
  }, 1000);
});

아래 데모를 실행해 보자. 점 P가 보간되면서 그려진 곡선을 2차 베지에 곡선이라고 한다.

See the Pen qrpYwj by Uyeong Ju (@uyeong) on CodePen.

수식 정리

우리가 2차 베지에 곡선을 위해 사용한 수식은 다음과 같다.

E = (s * A) + (t * B)
F = (s * B) + (t * C)
P = (s * E) + (t * F)

하지만 이 수식은 조금 장황하며 자바스크립트 코드상에서도 함수 호출이 빈번한 상태다. 이 수식을 방정식으로 좀더 간결하고 효율적으로 표현할 수 있다. 일단 연산식에 있는 괄호를 없애고 좀더 간략하게 수식을 표현한다.

E(t) = sA + tB
F(t) = sB + tC
P(t) = sE(t) + tF(t)

이번엔 중학생 때 배워본 몇 가지 곱셈 공식 사용하여 세 줄로 표현한 수식을 한 줄로 작성하고 이차방정식으로 정리한다.

P(t) = s(sA + tB) + t(sB + tC)
P(t) = (s²)A + (st)B + (st)B + (t²)C
P(t) = (s²)A + 2(st)B + (t²)C

자, 몇 가지 규칙을 더 추가하자. t가 0이라면 P는 항상 A와 같으며 다음과 같이 증명할 수 있다.

P(t) = (s²)A + 2(st)B + (t²)C
P(t) = (1²)A + 2(1 * 0)B + (0²)C
P(t) = (1)A + 2(0)B + (0)C
P(t) = (1)A
P(t) = A

다시 t가 1이라면 P는 항상 C와 같으며 다음과 같이 증명할 수 있다.

P(t) = (s²)A + 2(st)B + (t²)C
P(t) = (0²)A + 2(0 * 1)B + (1²)C
P(t) = (0)A + 2(0)B + (1)C
P(t) = (1)C
P(t) = C

이제 정리한 수식을 자바스크립트로 작성해보자. 함수명은 quadBezier로 짓고 2차 베지에 곡선임을 나타낸다.

function quadBezier(A, B, C, t) {
  if (t === 0) {
    return A;
  }
  
  if (t === 1) {
    return C;
  }
  
  const s = 1 - t;
  
  // (s²)A + 2(st)B + (t²)C
  return Math.pow(s, 2) * A + 2 * (s * t) * B + Math.pow(t, 2) * C;
}

이렇게 작성한 함수는 다음과 같이 사용할 수 있다.

interpolateBtn.addEventListener(\'click\', function() {
  // Start the interpolation.
  raf(function(t) {
    const x = quadBezier(posA.x, posB.x, posC.x, t);
    const y = quadBezier(posA.y, posB.y, posC.y, t);
    ...
  }, 1000);
});

3차 베지에 곡선

이제 3차 베지에 곡선(Cubic Bézier Curves)을 그려보자. 2차 베지에 곡선은 3개의 조절점을 이용해 그린 곡선을 말하듯 3차 베지에 곡선은 4개의 조절점을 이용해 그린 곡선을 말한다. 더 정확히는 두 개의 2차 베지에 곡선을 이용해 그린 곡선을 말한다.

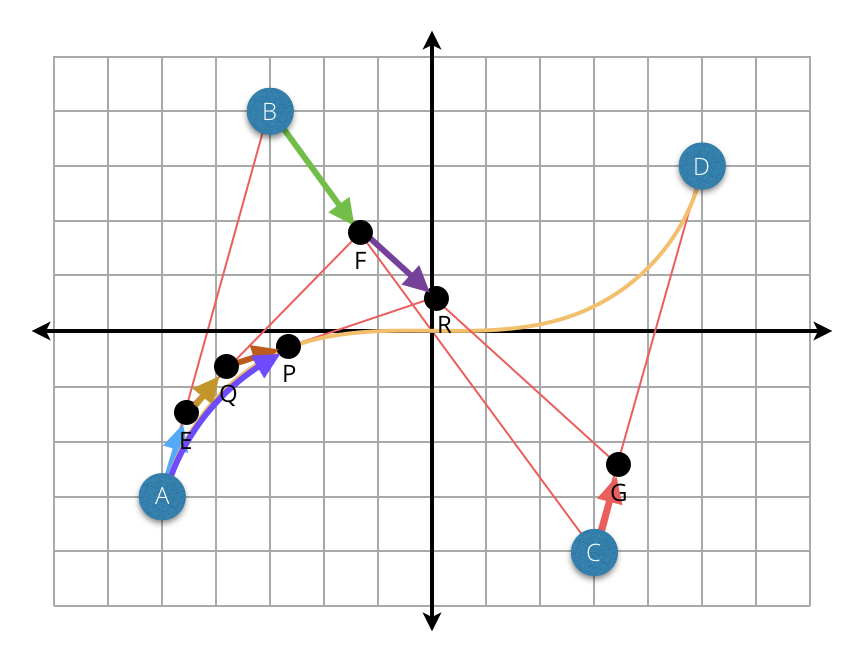
조절점 A, B, C를 이용해 그린 2차 베지에 곡선과 조절점 B, C, D를 이용해 그린 2차 베지에 곡선이 있다. 그리고 각 2차 베지에 곡선에서 보간되는 점 Q와 R이 있다. 이때 점 Q와 R를 이용해 또 다른 직선을 그릴 수 있고 이 직선에서 보간되는 점 P도 추가할 수 있다. 이제 점 Q와 R 그리고 P를 보간하면 P의 행적이 곡선을 만들어 낸다.

이제 3차 베지에 곡선을 직접 그려보자. 3차 베지에 곡선을 그리기 위해서는 보간되는 점 Q와 R 그리고 P를 구해야 한다. 점 Q는 다음과 같이 구할 수 있다.

E = (s * A) + (t * B)
F = (s * B) + (t * C)
Q = (s * E) + (t * F)

다시 점 R은 다음과 같이 구할 수 있다.

F = (s * B) + (t * C)
G = (s * C) + (t * D)
R = (s * F) + (t * G)

이제 점 Q와 R을 이용해 점 P를 구할 수 있다.

P = (s * Q) + (t * R)

이제 2차 베지에 곡선을 그릴 때 작성한 blend, blender 함수를 활용해 3차 베지에 곡선을 그려보자. 간단하게 새로운 점을 추가한 후 위에서 설명한 것처럼 점 Q, R, P를 구해 보간하면 된다.

아래 데모를 실행해 보자. 점 P가 보간되면서 그려진 곡선을 3차 베지에 곡선이라고 한다.

See the Pen EmOPJr by Uyeong Ju (@uyeong) on CodePen.

수식정리

점 Q와 P는 각각 2차 베지에 곡선에서 구해지는 점이므로 2차 베지에 곡선의 수식으로 표현할 수 있다.

Q(t) = (s²)A + 2(st)B + (t²)C
R(t) = (s²)B + 2(st)C + (t²)D
P(t) = sQ(t) + tR(t)

위 수식을 조금 더 풀어서 다음과 같이 정리할 수 있다.

P(t) = s((s²)A + 2(st)B + (t²)C) + t((s²)B + 2(st)C + (t²)D)
P(t) = s³A + 2(s²t)B + st²C + s²tB + 2(st²)C + t³D
P(t) = s³A + 3(s²t)B + 3(st²)C + t³D

이제 정리한 수식을 자바스크립트로 작성해보자. 함수명은 cubicBezier로 짓고 3차 베지에 곡선임을 나타낸다.

function cubicBezier(A, B, C, D, t) {
  if (t === 0) {
    return A;
  }
  
  if( t === 1) {
    return D;
  }
  
  const s = 1 - t;
  
  // P = s³A + 3(s²t)B + 3(st²)C + t³D  
  return (
    Math.pow(s, 3) * A + 
    3 * (Math.pow(s, 2) * t) * B + 
    3 * (s * Math.pow(t, 2)) * C + 
    Math.pow(t, 3) * D
  );
}

이렇게 작성한 함수는 다음과 같이 사용할 수 있다.

interpolateBtn.addEventListener(\'click\', function() {
  // Start the interpolation.
  raf(function(t) {
    const x = cubicBezier(posA.x, posB.x, posC.x, posD.x, t);
    const y = cubicBezier(posA.y, posB.y, posC.y, posD.y, t);
    ...
  }, 1000);
});

애니메이션

실제 동작하는 데모에서 requestAnimationFrame()을 사용해 일정한 시간마다 점을 찍는 것으로 3차 베지에 곡선을 그리고 있다. 그런데 곡선의 각 점이 찍히는 구간 즉, 보폭이 일정하지 않다.

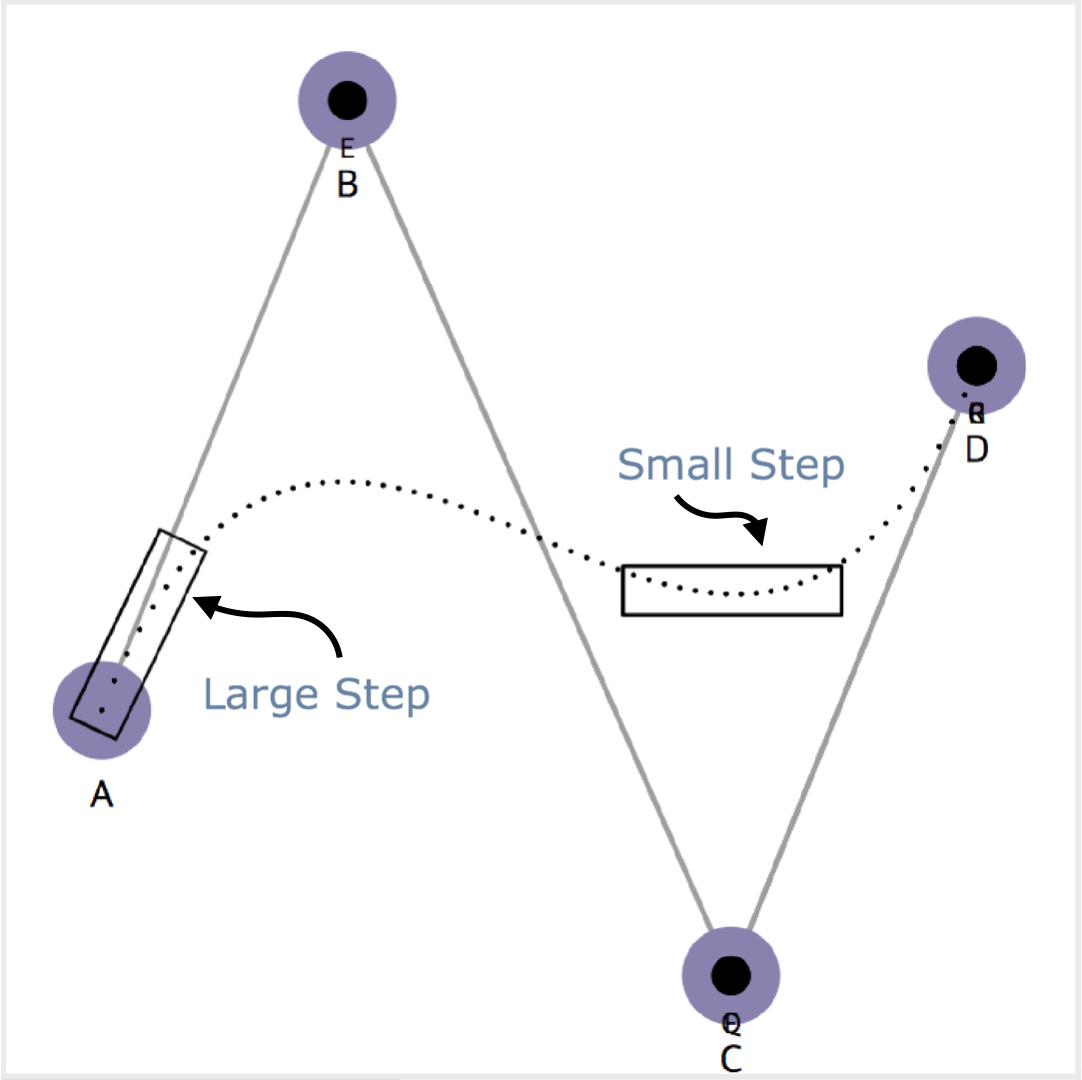
이러한 특징을 애니메이션 처리에 활용할 수 있다. 보폭이 크면 시간이 빠르게 흐르고 보폭이 작으면 시간이 천천히 흐르도록 표현하여 객체의 움직임에 역동성을 부여할 수 있다.

이제 CSS의 transition-timing-function의 cubic-bezier(Bx, By, Cx, Cy)가 의미하는 바가 무엇인지 또 어떻게 객체의 움직임에 활력을 불어넣을 수 있게 되는지도 이해할 수 있을 것이다.

끝으로

여기까지 베지에 곡선에 대한 연재 글을 모두 마친다. 처음엔 필자 역시 단순 호기심으로 시작했지만, 점점 원리를 알아가는 과정에서 상당한 재미를 느꼈다. 연재 글을 읽는 독자분들 역시 재미있는 경험이었길 바란다.