베지에 곡선과 관련된 수학적 증명 방법과 알고리즘은 1959년 프랑스의 자동차 업체 시트로엥(citroen)에서 근무하던 물리학자이자 수학자인 파울 드 카스텔조(Paul de Casteljau)가 최초 고안했다. 다른 말로 카스텔조 곡선(Casteljau curve)이라고 부른다.

하지만 시트로엥의 정책으로 인해 카스텔조가 얻은 성과가 1974년까지 발표되지 못했고 1962년에 프랑스 자동차 회사 르노(Renault)에서 근무하던 엔지니어 피에르 베지에(Pierre Bézier)가 자동차를 디자인하는 과정에서 이 곡선을 독자적으로 개발해 사용하면서 그의 이름으로 널리 알려지게 된다.

정의

베지에 곡선은 간단히 말해 복수의 조절점(Control point)을 이용해 매끄러운 곡선을 그릴 수 있는 가장 일반적인 매개 변수 곡선(Parametric curve) 이다. 매개 변수 곡선이란 매개 변수를 사용해 함수를 일반화하여 곡선을 그려내는 방법을 말한다.

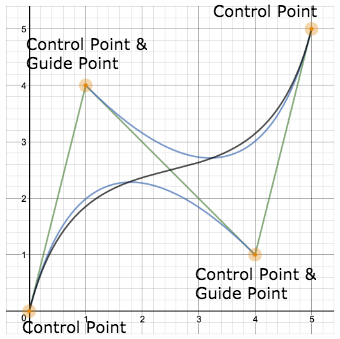
조절점이란 곡선의 모양을 결정하는 데 사용되는 점의 집합 또는 구성원을 뜻하며 가이드 포인트는 곡선의 모양을 변경시킬 수 있는 조절 가능한 점을 뜻한다. 그림 1의 점을 왼쪽부터 차례대로 P0, P1, P2, P3라고 할 때 보통 P0와 P3는 고정해두고 P1과 P2를 조절해 곡선을 변형한다. 이때 이 P1과 P2를 가이드 포인트라 한다.

베지에 곡선엔 차수가 붙는데 이 차수는 조절점의 개수에 따라 정해진다. 간단히 말해 N 개의 조절점으로 그려진 곡선을 N - 1차 베지에 곡선이라 한다. 예를 들어 그림 1은 조절점이 4개이므로 4 - 1 즉, 3차 베지에 곡선이다.

베지에 곡선이 그려지는 개괄적인 원리는 이전에 포스팅했던 「중학생도 알 수 있는 베지에 곡선(Bézier Curves)」을 참고하자. GIF 애니메이션을 이용해 이해하기 쉽게 설명돼 있다.

이번 편에서는 블렌딩(Blending)과 보간(Interpolcation)을 소개한다. 이 지식만 습득하면 나머지 n 차 베지에 곡선은 자연스럽게 이해할 수 있다.

에버리징과 블렌딩

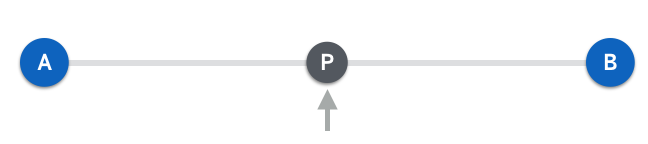
자, 위 그림 2와 같이 서로 떨어져 있는 점 A와 점 B가 있다고 해보자. 이때 점 P를 이 두 점 사이의 평균 즉, 선분의 중앙에 두고 싶다면 어떻게 해야 할까?

P = (A + B) / 2

위처럼 간단히 평균을 구해 중앙에 둘 수 있다. 이 수식을 조금 다르게 전개해보자.

P = (A + B) / 2
  = (A + B) * ½
  = ½A + ½B
  = .5A + .5B
  = (.5 * A) + (.5 * B)

위 수식을 이용한 연산을 블렌딩(Blending)이라고 표현한다. 지정된 각각의 비율에 맞춰 적절히 혼합하는 것이다. 자, 이제 같은 값이 아닌 가중치(Weights)를 줘서 블렌딩해보자.

P = (.35 * A) + (.65 * B)' 

이번엔 A는 0.35(35%), B는 0.65(65%)로 비율을 조정해 블렌딩했다. 이때 두 비율의 합은 당연하겠지만 1(100%)이 돼야 한다. 이것은 반드시 지켜져야 할 필수 조건이다. 이어서 비율 값을 다음과 같이 일반화해보자.

P = (s * A) + (t * B)' 

s는 A의 비율을, t는 B의 비율을 나타낸다. 만약 s가 높으면 t는 낮아지고 반대로 t가 높으면 s는 낮아질 것이다. 잠깐, s와 t는 서로 영향을 주며 두 수의 합은 항상 1이 돼야 한다. 그렇다면 s는 1 - t와 같다고 할 수 있다.

P = ((1-t) * A) + (t * B)' 

이제 변수 t 하나만으로 비율을 조정해 블렌딩할 수 있다. 이 수식은 다음과 같이 표현될 수 있다.

P = ((1 - t) * A) + (t * B)
  = (1 - t) * A + t * B
  = A - tA + tB
  = A + t(-A + B)
  = A + t(B - A)

이 글에서는 수식 P = (s * A) + (t * B)를 사용해 설명을 이어가겠다. 다시 한번 말하지만 s = 1 - t다. 여기에 몇 가지 규칙이 추가된다. 만약 변수 t가 0이라면 P는 항상 A와 같으므로 다음과 같이 표현될 수 있다.

P = ((1 - t) * A) + (t * B)
  = ((1 - 0) * A) + (0 * B)
  = (1 * A) + (0 * B)
  = A

또 변수 t가 1이라면 P는 항상 B와 같으므로 다음과 같이 표현될 수 있다.

P = ((1 - t) * A) + (t * B)
  = ((1 - 1) * A) + (1 * B)
  = (0 * A) + (1 * B)
  = A + B - A
  = B

이제 수식과 몇 가지 규칙을 참고하여 블렌딩하는 자바스크립트 함수를 작성해보자.

const A = 20;
const B = 198;

function blender(A, B, t) {
    if (t === 0) {
        return A;
    }

    if (t === 1) {
        return B;
    }

    return ((1 - t) * A) + (t * B); // or A + t * (B - A)
}

const blend = blender.bind(null, A, B);

console.log(blend(.0)); // 20
console.log(blend(.2)); // 55.6
console.log(blend(.4)); // 91.2
console.log(blend(.6)); // 126.8
console.log(blend(.8)); // 162.4
console.log(blend(1));  // 198

See the Pen qRBdvb by Uyeong Ju (@uyeong) on CodePen.

복합 데이터 블렌딩

이번에는 「에버리징과 블렌딩」 절에서 이해한 수식을 이용해 복합 데이터(Compound data)를 블렌딩해보자. 블렌딩 수식만 잘 활용하면 2차원 또는 3차원 같은 복합적인 데이터도 쉽게 블렌딩할 수 있다.

Px = (s * Ax) + (t * Bx)
Py = (s * Ay) + (t * By)
Pz = (s * Az) + (t * Bz)

3차원인 경우 위처럼 개별적으로 블렌딩한 후 연산된 값을 조합해 사용한다.

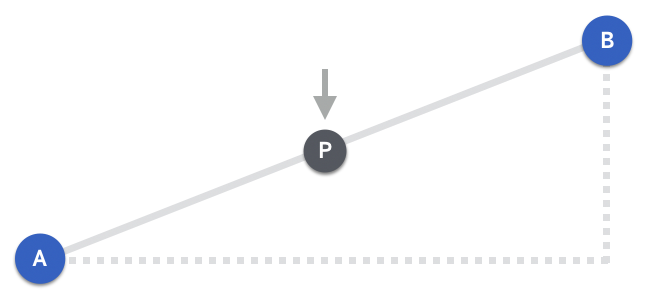
전 절에서는 점 A와 점 B가 동일 선상에 놓여있는 1차원적 상황이었지만 이번엔 그림 4 처럼 2차원 상황에서 P를 구해보자. 2차원에서는 x와 y 좌표로 점의 위치가 결정된다. 따라서 x와 y를 개별적으로 블렌딩한 후 구해진 값을 조합하면 P의 위치를 구할 수 있다.

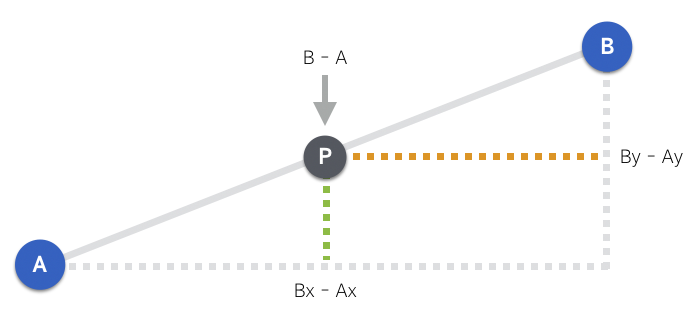
Px = (s * Ax) + (t * Bx)
Py = (s * Ay) + (t * By)
P = {Px, Py}

위 수식은 자바스크립트 코드로 다음과 같이 표현할 수 있다.

const Ax = 20;
const Ay = 144;
const Bx = 198;
const By = 72;

const blendX = blender.bind(null, Ax, Bx);
const blendY = blender.bind(null, Ay, By);

// t = .5
// P = { blendX(t), blendY(t) }

See the Pen EZxVVV by Uyeong Ju (@uyeong) on CodePen.

보간

마지막으로 보간(Interpolation)의 개념을 짤막하게 소개한다. 러핑(Lerping)이라고도 부르는 보간은 시간이 지남에 따라 블랜드 가중치를 변경하여 블렌딩을 수행하는 것을 말한다. 시간은 멈춰있지 않고 지속해서 흐르는 특징이 있으며 블랜드 가중치는 이 흐르는 시간에 의해 결정된다.

쉽게 말해 특정 값으로 블렌딩하는 게 아닌 지속해서 흐르는 시간에 근거해 블렌딩 하는 것이다. 이러한 과정은 대개 update()로 표현된다. 아래 자바스크립트 코드를 보자.

function interpolator(Ax, Bx, Ay, By, duration) {
  return function(update) {
  	 // x, y 블랜드 함수 준비
    const blendX = blender.bind(null, Ax, Bx);
    const blendY = blender.bind(null, Ay, By);
    
    ... 중략 ...
    
    function step(timestamp) {
      
      ... 중략 ...
      
      // 현재 시간에 해당하는 진행 값 즉, t 값 연산
      const pastTime = timestamp - startTime;
      let progress = pastTime / duration;

	   // t 값을 이용해 블렌딩하고 update 콜백 함수 호출
      update(blendX(progress), blendY(progress)); // Blending...

      ... 중략 ...
      
      requestAnimationFrame(step);
    }
    
    requestAnimationFrame(step);
  }
}

const interpolate = interpolator(Ax, Bx, Ay, By, 1000);

interpolate(function(nx, ny) {
	// 1초간 Interpolating.
	// P = {nx, ny}
});

우선 requestAnimationFrame()를 사용해 지정한 시간 만큼 흐르게 한다. 그리고 현재 시각에 해당하는 진행 값 즉, t를 구한 후 이 값을 근거해 블렌딩한다.

See the Pen dNbgQp by Uyeong Ju (@uyeong) on CodePen.

보간은 페이드인, 아웃 같은 애니메이션 처리나 3D 게임에서의 객체 움직임 그리고 오디오 크로스페이드 처리 등에 유용하게 사용된다.

여기까지 2편을 마치고, 다음 편에서 이 지식을 바탕으로 1, 2차 베지에 곡선을 소개하겠다.

참고

• Interpolation and Splines
• SMIL Animation
• Bézier curve - Wikipedia
• Paul de Casteljau - Wikipedia
• Pierre Bézier - Wikipedia
• Control point - Wikipedia
• Parametric curve - Wikipedia