“베지에 곡선”을 이용해 렌더링하게 되면 꽤 재미있고 편안하게 그림을 그릴 수 있다. 오늘은 이를 사용하는 누구라도 그 원리를 이해할 수 있도록 설명하고자 한다.

“베지에 곡선”이라는 것은 매끄러운 곡선을 그리기 위한 것이지만 설명은 우선 단순한 직선부터 시작하겠다. 아래 그림 1 처럼 직선에서의 점의 움직임이 모든 “베지에 곡선”의 기본이 되기 때문이다.

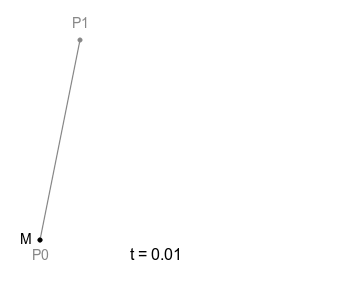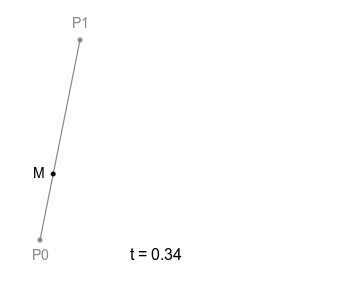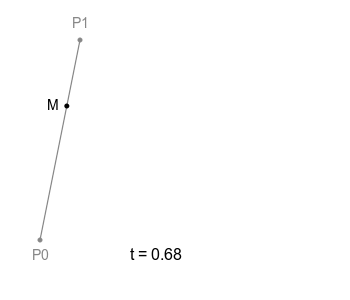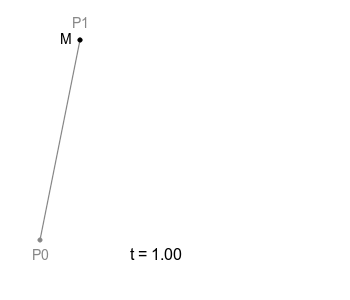
하나의 직선이 있고 그 위를 점 M이 일정 속도로 이동하고 있다. 이 점 M의 궤적은 당연하지만 단순한 직선으로 그려진다. 좋다. t는 선분 위를 비율적으로 얼마나 나아갔는지를 나타내는 수치다.

여기에 선을 하나 더 추가하고 그 위에 M처럼 이동하는 점을 놓아보자. 그리고 원래의 점 M을 M0로, 새로운 점을 M1으로 부르자. M0와 M1이 움직이는 규칙은 이전과 같다. M1이라는 점이 하나 더 늘었다 하더라도 특별히 복잡해질 것은 없다.

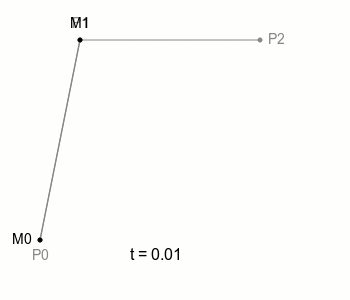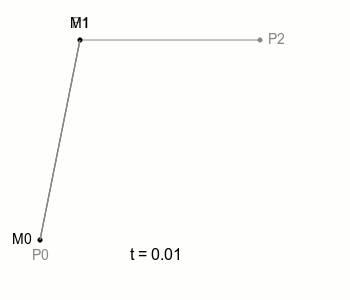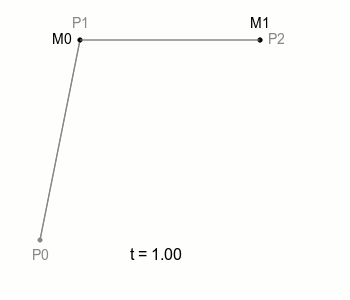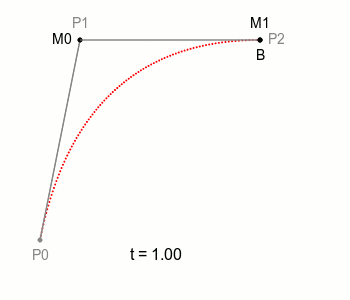
자, 여기에서 M0와 M1을 잇는 선을 하나 더 그을 수 있다. 그 선은 M0와 M1이 이동하면 자연스럽게 함께 움직이게 된다. 이제 그 선에 주목해보자. 그 선 위에 M0나 M1처럼 일정 속도로 이동하는 점을 놓을 수 있다. 그 점을 B라고 하자. 그리고 점 B가 그리는 궤적을 살펴보자. 그렇다. 점 B가 그리는 궤적을 **2차 베지에 곡선(Quadratic Bezier Curve)**이라고 한다.

점 P0, P1 등 을 조절점(Control Point)이라고 한다. 이제 조절점을 하나 더 늘린 “베지에 곡선”을 상상해보자.

아래 그림 3을 보면 새로운 점 P3가 추가돼 있고 P2와 P3를 선으로 잇고 있다. 그리고 M0나 M1과 같이 그 선 위를 이동하는 점을 생각해 볼 수 있다. 그 점의 이름은 M2라 하자.

자, 2차 베이제 곡선에서는 P0, P1, P2의 조합으로 점 B의 위치를 정할 수 있었다. 그렇다면 마찬가지로 P1, P2, P3의 조합으로도 비슷하게 점의 위치를 정할 수 있을 것이다.

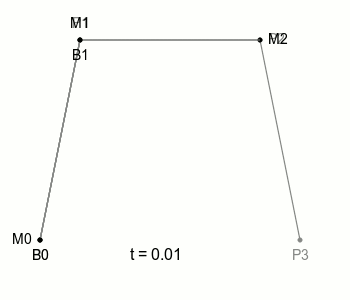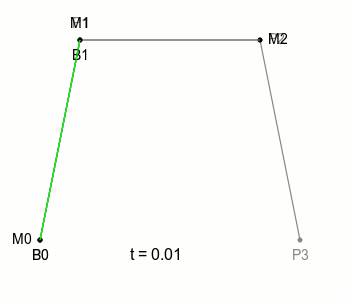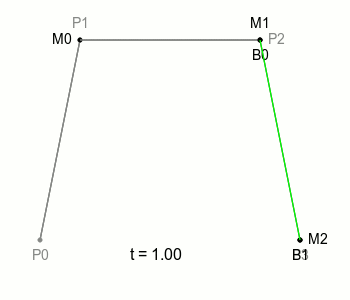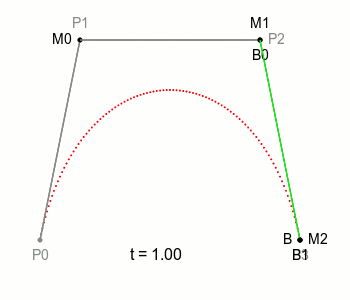
이전에 부르던 점 B를 B0라고 부르기로 하고 P1, P2, P3의 조합으로 정해지는 새로운 점을 B1이라고 부르기로 하자. 그렇게 하면 이전과 마찬가지로 점 B0와 점 B1을 잇는 선과 그 선 위를 일정한 속도로 움직이는 점을 다시 생각해 볼 수 있는데 이때 그 점이 그리는 궤적을 **3차 베지에 곡선(Cubic Bezier Curve)**이라고 한다.

여기에서 끝이 아니다. 조절점을 한 개 더 늘려 P0, P1, P2, P3 조합과 P1, P2, P3, P4 조합으로 결정되는 선과 그 선을 일정 속도로 이동하는 점 B2를 추가하고 B1과 B2를 잇는 선을 놓고 그 위를 지나가는 또 다른 점을 추가한 후 그 점이 그리는 궤적을 살펴볼 수 있다. 이런 식으로 곡선은 얼마든지 복잡하고 다양하게 만들 수 있다. P0부터 P4로 정해지는 곡선은 **4차 베지에 곡선(Quartic Bezier Curve)**이라고 부른다. 하지만 조절점을 5개 이상 늘려도 실용적인 측면에서 특별한 이점이 없으므로 일반적으로 3차 베지에 곡선까지 사용된다.

여기까지 간단하게 “베지에 곡선”에 관해 이야기했다. 한마디로 “베지에 곡선”이란 선분 위를 일정 속도로 움직이는 점과 그러한 점과 점을 잇는 또 다른 선분, 그리고 그 위를 일정 속도로 이동하는 또 다른 점 등을 조합해 최종적으로 특정 점이 그리는 궤적을 이용해 곡선을 그려내는 방법을 뜻한다. 이해하는 데 도움이 됐으리라 기대한다.